효과적인 공식 암기를 위한 습관
제가 학생들을 가르치면서 학생들에게 가장 많이 들었던 이야기 중 하나가 ‘이때
무슨 공식을 쓰는지 까먹었어요’ 입니다. 사실 수학 시험을
볼 때에는, 그 단원에서 배웠던 것만 물어보는 것이 아니라, 예전에
배웠던 개념을 같이 물어보는 경우가 많습니다. 그런데 적분 단원 문제를 푸는데 미분에서 사용되는 공식을 제대로 기억하지 못해서 문제를 못풀고, 원의 방정식을 제대로 기억하지 못해서 틀린다면 고득점을 기대하기 힙듭니다. 그렇다면 이제 어떻게 공부를 해야지 공식을 제대로 익힐 수 있는지 봐봅시다.
1. 단순히 공식만 암기하지 말자
제가 과외를 하면서 느낀 점은, '공식만이라도 제대로 기억하고 있는 학생이 드물다'라는 것이었습니다.
시험이나 숙제에서 틀린 문제,
못푼 문제를 같이 풀어볼 때 문제에서 주어진 조건을 가지고 식을 정리해 주면서, 중간중간
공식을 사용해야 할 때 ‘자 이때 어떤 공식 써야돼?’ 라고
물어봤을 때에 제대로 대답하는 학생이 드물었습니다. 부호를 헷갈려 한다던지 절댓값, 루트 기호를 빼먹는다던지 하는 식으로 공식을 완벽하게 기억하지 못하는 학생이 대부분이었습니다.
흥미로운 것은 그런 학생들은 공식을 계속 못외운다는 것입니다. 심지어 수능을 치기 직전까지요. 그 학생들이라고 해서 공식을 외우기
싫은것도 아닐텐데, 왜 그 공식을 계속 못외우는걸까요? 그건
공식만 암기하기 때문입니다.
일차적으로, 수학
공식 자체에는 큰 의미가 없습니다. 여러분들이 그 의미를 이해하지 못한다면 그건 공식이 아니라 단순한
문자의 나열일 뿐입니다. 그렇다면 여러분들은 그 공식이 어떻게 유도됐고, 어떤 조건이 필요한지에 대해서 정확하게 알고 있어야 하는데, 이건
단순히 공식을 외운다고 얻어지는 것이 아닙니다. 따라서 여러분들은 교과서를 다시 펴서, 공식을 설명하기 전 개념을 다시 한번 읽어보고, 유도 과정을 직접
손으로 따라 써 보며 공식을 종합적으로 이해해보려고 하세요.
그리고, 공식을 어느
정도 이해했다는 생각이 든다면 좀 더 깊게 파보세요. 문제의 공식이 왜 그렇게 정의가 됐는지, 역은 성립하는지 안하는지, 성립하지 않는다면 왜 성립하지 않는지, 이런것들까지 꼼꼼하게 복습해야 여러분들의 머리속에 공식과 개념이 정확하게 남을 것입니다.

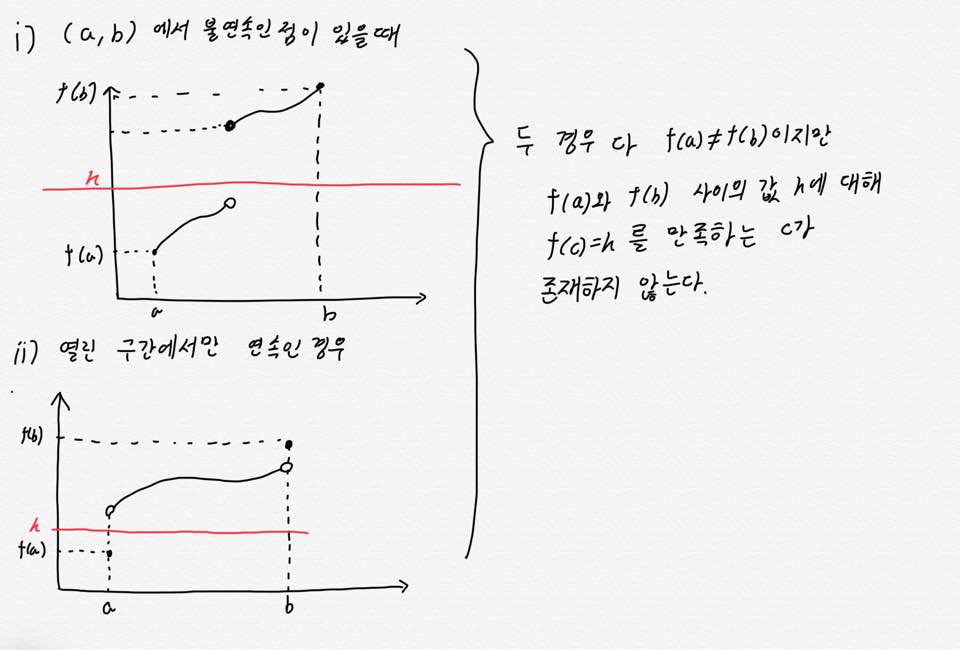
위의 교과서 캡처에 적힌 내용을 보면 닫힌 구간에서 연속인 함수라고
돼있지요? 그렇다면 왜 열린 구간이 아니라 닫힌 구간인지, 왜
연속인 함수인지 그 밑의 그림과 같이 그래프를 그려가면서 확인해 봐야 합니다. 이처럼 공식을 단순히
외우는 것이 아니라 깊게 탐구해 보아야 실제 문제풀이에도 공식을 쉽게 적용할 수 있을 것입니다.
2.
백지 복습
수학에서 배우는 개념들은 서로 유기적으로 연결되어 있습니다. 그 개념들을 유기적으로 연결시킬 수 있다면, 문제를 풀 때 관련
개념을 끄집어 내기 더 쉬울 것입니다. 이때 유용한게 백지 복습입니다.
문제를 풀다가 어떤 개념이 잘 떠오르지 않았다면, 먼저 그 개념을 적어 보세요. 그리고 그 개념에서 유도할 수 있는 다른 개념들을 마인드맵 형식으로 쭉 적어보면서 복습해보세요. 이렇게 복습해 본다면, 문제를 풀 때에도 연관 개념들을 잘 생각할
수 있을 것입니다.
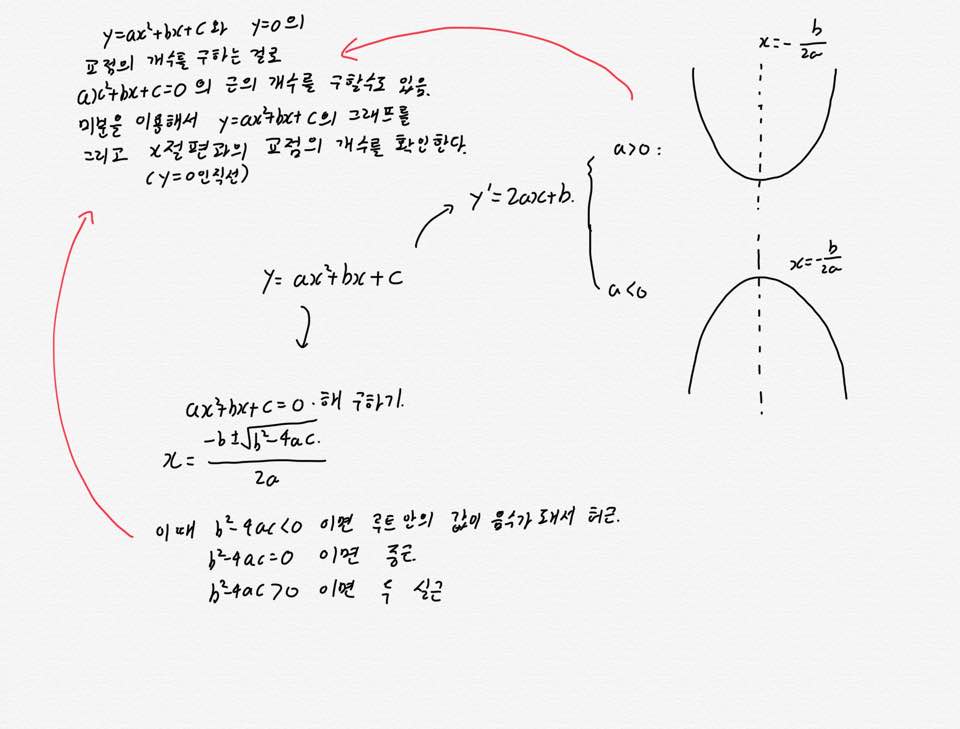
위에서 제가 그린 백지복습을 봐봅시다. 맨 처음엔 단순히 이차함수의 공식에서 시작했습니다. 하지만 그걸 이용해서 이차방정식의 해, 판별식의 조건, 미분을 이용해서 꼭지점을 구하는 방법, 그래프를 활용해서 근을 구하는 방법 등을 유도해 볼 수 있습니다.여러분들이 직접 백지복습을 해볼때에는 저정도만 하지 마시고, 관련된 개념을 최대한 많이 적어보려고 해보세요. 그리고 그 개념들이 왜 어떻게 연관되는지 설명하지 못한다면 다시 한번 교과서를 펴서 공부하세요.
여러분들이 이렇게 공부하다 보면, 실제 시험에서도 문제를 풀 때 사용해야 하는 개념을 좀 더 빠르고, 정확하게 연상할 수 있을 것입니다.





