순열/조합/확률을 체계적으로 잘하는법
순열, 조합, 확률 문제를
유독 어려워하는 학생들이 많습니다. 다른 단원 문제는 잘 풀어도, 순열조합확률에서
어렵게 나오면 틀리는데 또 어떻게 공부를 해야 할지 잘 모르는 학생들은 이렇게 공부해 보기 바랍니다. 우선
순열, 조합, 확률 문제를 어려워하는 이유는 다음과 같습니다.
1. 개념과 응용문제 사이의 괴리가 크다
순열, 조합, 확률에서
개념만을 익히는 것은 크게 어렵지 않습니다. 미적분에서 배웠던 복잡한 개념들에 비하면, 훨씬 익히기도 쉽고 공식도 몇 개 없습니다. 하지만 기출문제를 보면
그 쉽게 배웠던 개념이 정말 다양하고, 심화된 방식으로 응용되어서 나오면서 막히게 됩니다.
2. 경우의 수를 놓쳐서 실수하기 쉽다.
공부를 해본 학생들이라면 잘 알고 있겠지만, 순열, 조합, 확률 문제에서 틀렸을 때 가장 많이 하는 말 중 하나가 ‘아 이거 빼먹었다’입니다. 경우의
수를 세는 단원이기 때문에 그런 일은 자주 있을 수밖에 없습니다. 다른 단원에서는 경우의 수를 고려하여서
문제를 푸는 경우가 거의 없기 때문에, 경우의 수를 하나라도 놓치면 틀리는 순열, 조합, 확률 문제가 더 생소하고,
어렵게 느껴질 수밖에 없습니다.
그렇다면 이 1,2번 문제를 어떻게 해야할지 봐봅시다.
1.
개념보다는 문제풀이 비중을 높이자.
수학에서 개념 공부는 중요합니다. 하지만 순열/조합/확률에서는
개념 자체가 어렵다기 보다는, 응용이 더 어렵고 다양한 케이스를 익혀 보는 것이 중요하기 때문에 문제를
많이 풀어보는 것을 추천합니다. 그것도 하루에 몰아서 하는 것이 아니라, 하루에 5~10문제씩 매일매일 꾸준히 풀어보세요. 그러면서 어떤 경우에 중복순열, 중복조합, 원순열… 등등이 적용되는지 익혀보는게 필요합니다.
2.
케이스 분류를 하면서 풀어보자
개인적으로는 제일 중요하다고 생각하는 방법입니다. 위에서 말했던 것처럼 경우의 수를 하나도 빼놓기 않게 세는 것은 쉽지 않습니다. 그래서 명확한 기준을 가지고 나눠 주면서, 그 상황에 맞는 경우의
수를 계산하는 연습을 해야 합니다.
작년 수능 기출문제로 한번 예를 들어 봅시다.
홀수 1,3,5와
짝수 2,4,6을 문제에서 주어진 조건을 다 활용하면서 경우의 수를 한번에 구하기는 쉽지 않습니다. 따라서 문제의 조건을 만족하는 케이스를 하나 하나 구해보면서 그에 해당하는 경우의 수를 구했습니다. 여러분도 순열조합 문제를 풀 때 이처럼 케이스 분류를 하나하나 해보면서 풀어보세요.
3.
하나하나에 의미를 적기
순열/조합/확률 문제를 풀 때에는 복잡한 연산을 쓰지 않습니다. 사칙연산이 전부입니다. 그러다 보니 계산을 하다 보면 자신이 뭘 하고 있는지 헷갈릴수도 있고, 그러다
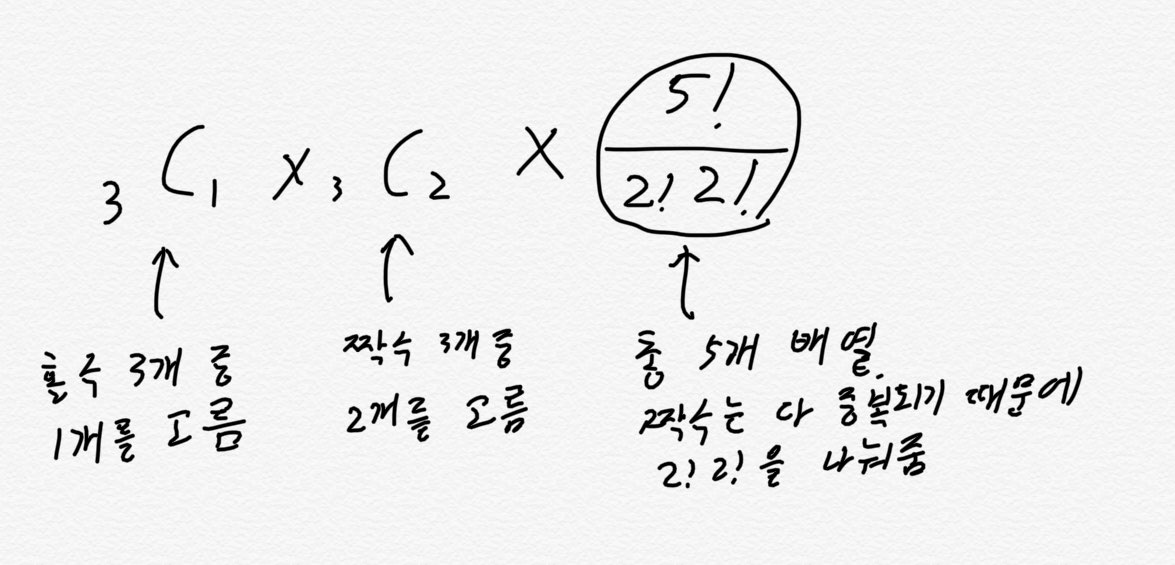
보면 놓치거나 중복돼서 계산할 수도 있습니다. 따라서 위 문제의 1번
케이스를 구할 때에도, 단순히 3C1 <-이렇게 간단하게만 적는 것이
아니라 다음과 같이 적어보세요.
사실 이렇게 간단한 문제는 저렇게 하나 하나 의미를 적으면서
풀지 않아도 괜찮지만, 문제가 복잡해질수록 내가 지금까지 구한게 뭐고,
앞으로 구해야 할 것이 뭔지 명확하게 파악하기 어렵습니다. 그러니 이렇게 숫자 하나 하나가
어떤 의미를 가지는 지 정리해서 적어보고, 스스로 머리속에서 풀이를 정리해 보세요. 이제 어떤 것을 구했으니, 앞으로는 무엇을 구해야 하고, 중복되거나 빠지지 않게 하려면 어떻게 해야 할지…
이렇게 알려드린 방법대로 매일 꾸준히 연습하다 보면 여러분들은 순열/조합/확률 문제를 어려워하지 않을 것이라고 확신합니다.


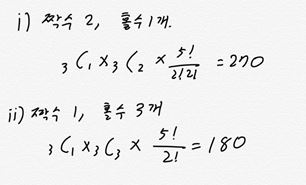



![[비교과 준비 노하우] 서울대 경제학과 최초합 생기부 대공개!](https://www.supaja.com/image/bbs/teacher/bbs_5F4556FD66440_20200825182253.jpg)
