수파자
네이버로 로그인올바른 개념 공부법
그동안 학생들을 가르쳐 오면서 느낀 수학을 어려워하는 학생들의 가장 큰 특징은 개념공부를 소홀히 한다는 것입니다.
처음에 교과서나 개념서(수학의 정석,
바이블)에 설명되어있는 개념 설명을 제대로 공부하지 않고, 단순히 공식만 외운 다음에 그 공식을 어찌어찌 대입해서 문제풀이만 하면서 공부하려고 하는 학생들을 많이 봤습니다.
그런 식으로 공부를 한다면 교과서 예제 수준의 쉬운 문제는 풀 수 있을지 몰라도,
고득점을 위해 반드시 풀어야 하는 고난이도 문제를 풀 수는 없습니다.
또한 학년이 올라가면 올라갈수록 공부한 단원은 늘어나고,
그러다 보면 문제를 풀 때 적용해야 하는 공식을 정확하게 기억하기조차 쉽지 않습니다.
영어 단어도 처음 외울 때 단순하게 외우는 것보다 접두사, 접미사가 어떻게 연결되어서 단어의 뜻이 형성되는지 이해하는 것이 더 효율적이듯, 수학도 개념에 대한 정확한 이해가 되어 있어야 기억하기도 쉽고,
문제를 풀 때 풀이법을 생각하기도 쉽습니다.
그럼 교과서/개념서를 공부할 때 다음과 같이 공부해보는걸 추천드립니다.
1. 무엇을 구하기 위한 것인가?
시험장에서 심화 문제를 풀 때 주어진 조건에 필요한 공식을 제대로 떠올리지 못해서 문제를 푼 경우가 있을 겁니다. 그런 상황은 문제를 많이 풀어 보지 못해서가 아니라, 개념 공부를 소홀이 했기 때문입니다.
먼저 교과서의 학습 목표를 보고, 교과서에서 설명하는 공식이 무엇을 구하기 위한 것인지를 잘 생각해보길 바랍니다.
그렇다면 어떤 느낌으로 개념에 접근해야 할 지 알 수 있습니다.
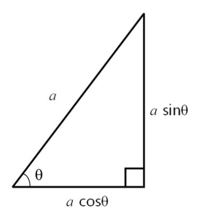
삼각함수의 공식을 배울 때를 생각해 봅시다. 삼각함수에서는 다음 그림과 같은 직각삼각형이 있을 때 높이를 a*sinθ, 밑변의 길이를 a*cosθ로 나타낼 수 있다는 것을 알 수 있습니다.
그렇다면 처음 삼각함수를 배울 때에 단순히 ‘직각삼각형이 있고 빗변의 길이가 a라면 높이는 a*sinθ, 밑변의 길이는 a*cosθ…’ 이런 식으로 단순 암기만 하는 것이 아니라, ‘직각삼각형의 한 변의 길이와 한 각의 크기가 주어진다면, 나머지 두 변의 길이도 주어진 길이와 각의 크기를 활용해서 표현할 수 있다.’ 라는 것까지 생각하는 것이 중요합니다. 이처럼 처음 개념을 배울 때에 공식만을 외우는 것이 아니라, 공식이 무엇을 구하기 위한 것인지 그 의미를 함께 생각해 본다면, 실제로 시험장에서 문제를 풀 때 상황에 맞는 공식을 잘 떠올릴 수 있을 것입니다.
2. 공식이 어떻게 유도되는가?
많은 학생들은 공식을 유도하는 것을 어렵고 필요없다고 생각해서 그냥 넘어가는 경우가 많습니다. 그러나 교과서에서 나오는 공식들을 유도할 줄 안다면, 공식을 외우는 과정도 수월할 뿐더러,
시험장에서 공식이 헷갈리더라도 금방 유도할 수 있습니다.
삼각함수에서 설명하는 공식들을 봅시다. 무작정 외우기에는 많을 뿐만 아니라 외우고 나서도 헷갈릴 수 있는 부분도 많습니다. 그러나 단위원을 활용하여서 유도할 수 있다면 핵심 정리 하나만 가지고도 시험장에서 자신이 기억한 공식이 정확한지 점검할 수 있습니다
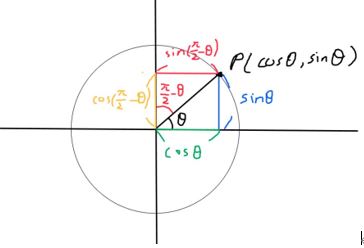
단위원을 활용해서 코사인, 사인의 덧셈 , 뺄셈공식을 유도해 봅시다.
단위원(반지름의 길이가 1이고 중심이 원점에 있는 점) 위의 한 점 P의 x좌표는 cosθ, y좌표는 sinθ로 나타낼 수 있습니다. 이걸 이용해서 sin(/2 - θ)를 구한다면, θ가 예각인 경우에는 위의 그림과 같이 단위원 위에 sin(/2 - θ)의 값을 표시할 수 있습니다.
/2 - sin(/2 - θ)에 해당하는 빨간색 선의 길이가 cosθ에 해당하는 초록색 선의 길이와 일치하기 때문에, sin(/2 - θ) = cosθ 공식이 성립한다는 것을 알 수 있습니다.
이처럼 공식을 너무 억지로 외울려고만 하지 말고, 어떻게 유도되는지 확인해 보면서 공부한다면 공식 암기에 대한 부담도 줄어들고 잘 외워질 뿐만 아니라 시험장에서 공식을 까먹더라도 유도한다음 풀 수 있을 것입니다.
3. 다른 단원에서 배웠던 개념도 활용할 수 있는가?
다른 단원의 개념을 활용해서 증명할 수 있다면 개념을 좀 더 깊게
이 글은 이런 분들에게 추천해요: 1. 내신 성적이 항상 2% 부족한 느낌을 받는 학생 2. 공부 자극받고 싶은 학생 안녕하세요, 저는 서울대학교 소비자아동학부에 소비...
여러분들은 수험 기간동안 받은 스트레스를 어떻게 푸시나요? 각자 나름대로의 스트레스 해소법이 있겠지만 2020 수능 만점자 홍민영 선생님의 방식은 어떨지 궁금하시지 않나요? 영상...
현재 수파자에서 활동 중인 2020 수능 만점자 홍민영 선생님께서 알려주시는 공부에 있어 질과 양 중 어떤 것이 더 중요한 지에 대한 설명 영상입니다. 영상의 내용이 궁금하시다면 ...
많은 학생들이 모의고사를 치고 나서 점수에 신경을 많이 씁니다.하지만 제가 학생들을 가르치면서 느낀 것은, 모의고사 점수에 연연하는 학생은 많지만 실제로 모의고사를 치고 난 후 올...